Whether you’re a student revising key texts, a parent supporting at home, or a teacher planning next term’s lessons, understanding what’s expected in GCSE Maths is essential.
This guide breaks down the core topics, skills and assessment style for 2026, with practical examples and revision strategies to support confident preparation at home or in the classroom.
What this article covers:
- Full topic list for GCSE Maths (Foundation and Higher tiers)
- Key learning objectives for each topic
- Sample questions and exam-style practice
- Study tips to boost your marks
Why maths matters for GCSE success
GCSE Maths is one of the most important GCSE subjects; it’s required for most college courses, apprenticeships, and jobs. Many sixth forms and further education providers want at least a grade 4, which is a standard pass. Some A level subjects, like sciences or economics, may need a grade 6 or higher.
A strong GCSE Maths grade also opens the door to careers in:
- Engineering, architecture, and construction
- Finance, accountancy, and data analysis
- Teaching, science, and healthcare
- Tech roles like programming and software development
Overview of the 2026 GCSE Maths exam
The 2026 GCSE Maths exams will follow the current rules from the main exam boards: AQA, Edexcel, OCR, and WJEC. Each board assesses the same core content, with slight variations in question phrasing and structure.
Exam structure:
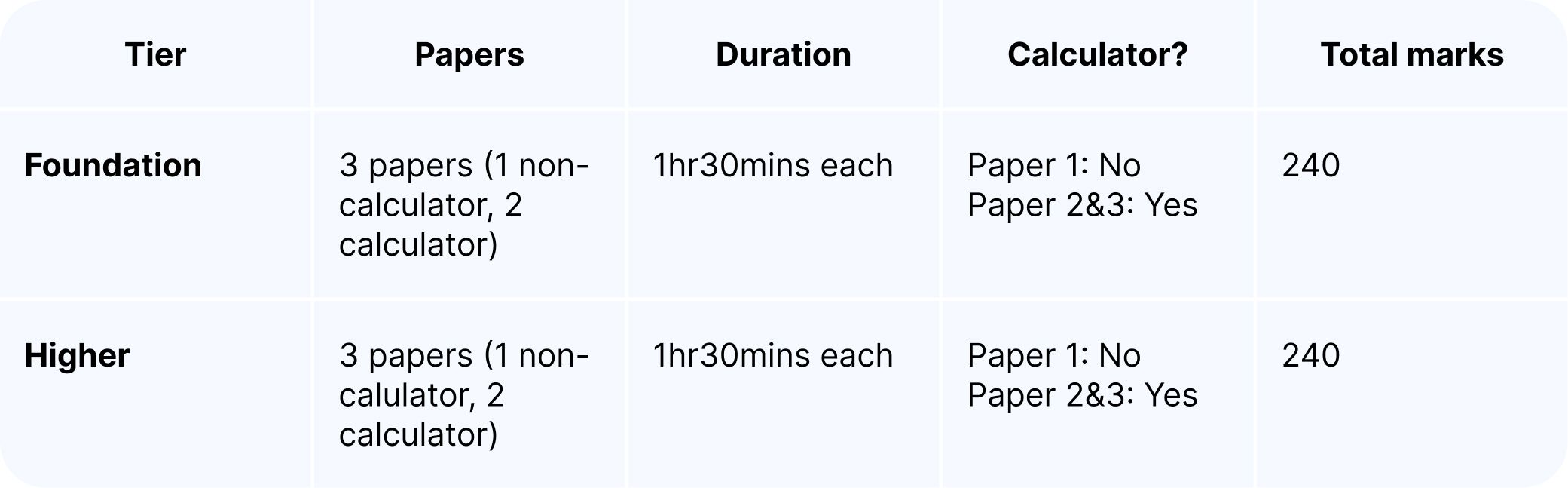
Core GCSE Maths topics (Foundation & Higher)
GCSE Maths content is split across six broad domains. Here’s what students need to cover, with Foundation and Higher tier examples to show how the difficulty can vary.
1. Number
Learning objectives:
- Apply place value, rounding, and estimation
- Work with fractions, decimals, and percentages
- Use ratio and proportion
- Apply powers, roots, and standard form
Sample question:
Foundation:
What is 25% of 160?
Answer: 40
Higher:
Write 3,600,000 in standard form and evaluate: (3.6 × 10⁶) ÷ (1.2 × 10³)
Answer: 3 × 10³
2. Algebra
Learning objectives:
- Simplify expressions, solve equations, and rearrange formulae
- Plot graphs and interpret relationships
- Work with sequences, inequalities, and algebraic proof
Sample questions:
Foundation:
Solve: 2x + 5 = 17
Answer: x = 6
Higher:
Factorise: x² − 5x − 24
Answer: (x − 8)(x + 3)
3. Ratio, proportion and rates of change
Learning objectives:
- Solve problems using direct and inverse proportion
- Use percentages in context (e.g. growth/decay)
- Interpret compound measures like speed and density
Sample questions:
Foundation:
A recipe uses 300g of flour for 4 servings. How much flour is needed for 6 servings?
Answer: 450g
Higher:
A car travels 180 km in 2 hours 15 minutes. What is its average speed in km/h?
Answer: 80 km/h
4. Geometry and measures
Learning objectives:
- Use angle facts, properties of shapes, and symmetry
- Apply Pythagoras’ theorem and trigonometry
- Calculate perimeter, area, volume, and surface area
Sample questions:
Foundation:
Find the perimeter of a rectangle with sides 5 cm and 8 cm.
Answer: 26 cm
Higher:
A triangle has sides 7 cm and 9 cm with an included angle of 60°. Use the cosine rule to find the third side.
Answer: c² = 7² + 9² − 2×7×9×cos(60) → c ≈ 7.6 cm
5. Probability
Learning objectives:
- Understand and calculate probabilities from tables, lists, and diagrams
- Use Venn diagrams and tree diagrams
- Know the laws of probability (mutually exclusive and independent events)
Sample questions:
Foundation:
A bag contains 5 red balls and 3 blue balls. What is the probability of picking a red ball?
Answer: 5/8
Higher:
Two biased coins are flipped. The probability of heads on each is 0.6. Find the probability of getting exactly one head.
Answer: 0.6 × 0.4 + 0.4 × 0.6 = 0.48
6. Statistics
Learning objectives:
- Interpret and create charts, graphs, and tables
- Calculate averages and range
- Understand sampling, correlation, and distributions
Sample questions:
Foundation:
Find the median of: 3, 7, 8, 12, 15
Answer: 8
Higher:
A grouped frequency table shows the number of hours 20 students revised. Estimate the mean number of hours.
(A frequency table would be provided)
Answer: Use midpoints × frequency, then divide total by 20